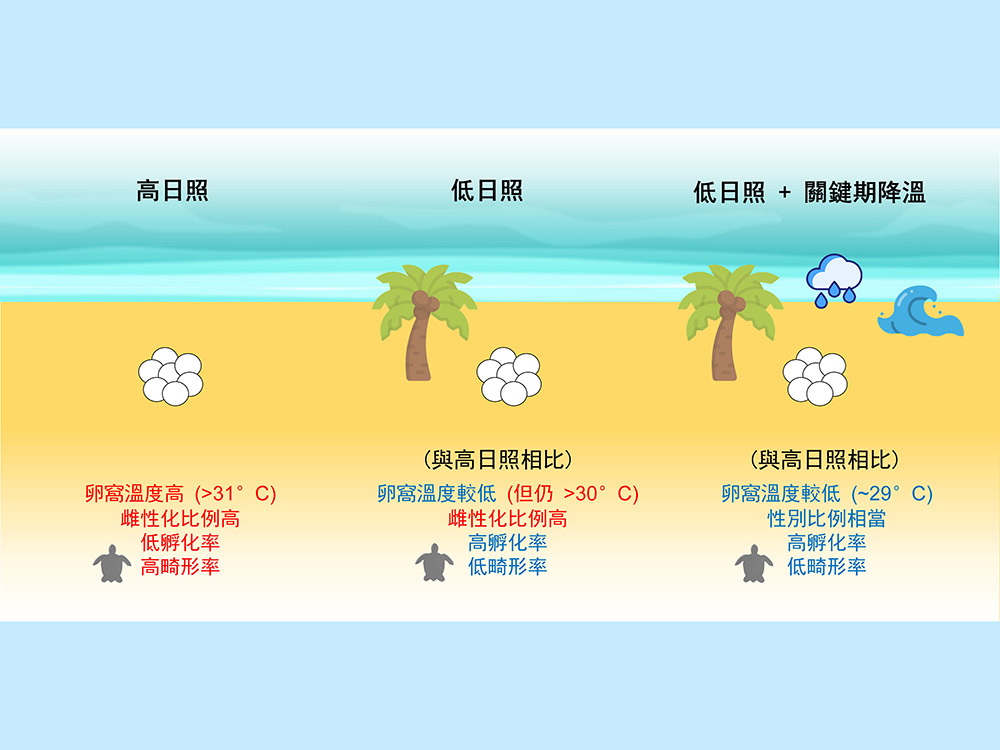
生命科學院柯佳吟教授團隊 監測暖化對國境之南綠蠵龜孵化的衝擊
瀏覽器版本過舊,或未開啟 javascript
請更新瀏覽器或啟用 javascript
圖一 引自 google EDL圖片
圖二 鈉、鎂濃度比與內部、邊界電位公式
圖三 引自Nature 415, 213-218 (2002)(PNP)方程組
圖四 鉀離子通道結構與多域網格multi-domain
(文:林太家教授 )
數學建模是以數學精煉的語言來描述解決各類問題的思想和方法,是應用數學與其他學科連接的橋樑,在跨領域學科研究中扮演重要地位。本校自2011年至今先後成立臺大理論科學研究中心(2011年)、應用數學科學研究所(2013年),並爭取科技部國家理論科學中心數學組到本系(2015年),期間本系在發展跨領域學科研究方面不遺餘力,與本校大氣系、工科海洋系、應用力學所、海研所等系所有關老師合作研究並定期舉辦學術活動。預期未來應用數學能在本校深耕發展,培育優秀人才。
數學分析與數值模擬在數學建模之建構與驗證上至關重要。本文將以電雙層與離子通道數學建模為例,分述如下:
電雙層Electric Double Layer (EDL) 的概念由亥姆霍茲(Helmholtz)於1879 年首先提出,並在1950 年Grahame 提出理論上的根據。 EDL是在帶電表面形成的電荷積聚/分離的結構,由於帶電表面的性質和電場對離子遷移的影響,附著於帶電表面的EDL(如圖一)。在電化學中,邊界層問題的產生主要是為了處理電雙層的微觀現象,如半導體、 電動流體和電解液中的微觀現象。 特別地,薄EDL 是作為新型儲能裝置(通常稱為超級電容器)的大容量電化學電容器,這使得EDL的建模、分析與模擬成為一個重要的問題。
傳統上,泊松-能斯特-普朗克Poisson-Nernst-Planck (PNP)方程組是描述離子傳輸機制的經典模型。我們運用弗拉索夫-泊松-褔克-普朗克Vlasov-Poisson-Fokker-Planck 方程組推導動力學理論kinetic theory證明PNP方程組是在不考慮離子大小size情況下描述離子傳輸機制的合理模型[1]。因此可以用PNP方程組描述電雙層(EDL)中離子分佈較稀(dilute)的漫射層(diffuse layer),推導平衡態邊界層(boundary layer)解的近似理論[2]與穩定性理論[3]。此外關於鈉、鎂、氯混合溶液,我們以嚴格的數學分析證明出鈉、鎂濃度比與內部、邊界電位公式(圖二)並獲得實驗證實[4]。
離子通道(ion channel) 是一種蛋白質結構,如同一個可以開關的「門」存在於細胞的細胞膜上(如圖三)。它通過允許某種特定類型離子穿過該通道來調控細胞膜內的離子濃度,在生物和醫學上扮演非常重要的角色。理解離子通道運作的原理,傳統上是以分子動力Molecule Dynamics (MD)模擬法並利用電腦程式的計算來模擬通道內的離子動態。此法雖被大多數生物學家採用,但描述所有離子動態之常微分方程組卻非常龐大且複雜,所需計算時間十分冗長。因此尋找有效率的數學建模來模擬離子通道內離子傳輸(ion transport),成為一個有趣且重要的問題。然而傳統PNP方程組無法模擬出通道的選擇性(selectivity)與開關(gating)機制,因此這個模型有修正的必要。
圖三 引自Nature 415, 213-218 (2002)(PNP)方程組主要包括靜電位能(electrostatic potential)與漂移擴散(drift diffusion)的作用 ,與分子動力模擬(MD)相比主要缺少了李納-瓊斯位能Lennard-Jones (LJ) potential的作用。因此如何把LJ位能的作用加入PNP方程組便成為一個有趣的問題。我們利用傅利葉分析法 (method of Fourier analysis)建構近似LJ位能 (approximate LJ potential),推導出對應的交叉擴散 (cross-diffusion) 項並用以修正原PNP方程組為具空間效應(steric effect)之PNP-steric方程組[5]。在數學分析方面,我們找到控制PNP-steric平衡態方程組的代數結構,結合非線性橢圓方程式分析技巧,證明多重平衡態的存在性並推導溢電流公式,作為以PNP-steric方程組來研究開關機制的理論基礎[6]。在數值模擬方面,運用PNP-steric 方程組成功模擬出通道的選擇性[7]與開關機制[8]。此外為處理離子通道複雜的幾何結構,蔡秉軒(應數所碩士2017年7月畢,2018年3月申請到布朗大學、伊利諾大學香檳分校博士班全額獎學金)發展三維多域網格multi-domain之數值計算法,這項研究成果獲美國Argonne國家實驗室(ANL)的重視,邀請他和藍鈺翔(應數所碩二生)於2017年暑期前往ANL合作研究,以高性能計算High Performance Computing 設計精確且有效的運算程式來模擬PNP-steric方程組和鉀離子通道複雜的幾何結構(如圖四)。
結論
以數學分析、數值模擬方法獲得創新的數學建模,用來研究離子通道與電雙層,產生在數學和科學上都有價值的成果。預期本系未來在數學建模之分析與模擬能與更多系所合作,共創雙贏。
文獻索引
[1] H. Wu, T.C. Lin and C. Liu, Diffusion limit of kinetic equations for multiple species charged particles, Arch. Rational Mech. Anal. 215 (2015) 419–441.
[2] C. C. Lee, H. Lee, Y. Hyon, T. C. Lin and C. Liu, Boundary layer solutions of charge conserving Poisson-Boltzmann equations: one dimensional case, Comm. Math. Sci. Vol. 14, No.4 (2016), 911-940.
[3] C.Y. Hsieh and T.C. Lin, Exponential decay estimates for the stability of boundary layer solutions to Poisson-Nernst-Planck systems: one spatial dimension case, SIAM J. Math. Anal. Vol.47, No.5 (2015), pp. 3442–3465.
[4] 黃崧任、吳政晏, 測量電雙層電位、緊密層厚度及離子濃度之方法,中華民國專利公告號:I571640,公告日:2017/02/21。
[5] T.C. Lin and B. Eisenberg, A new approach to the Lennard-Jones potential and a new model: PNP-steric equations, Communications in Mathematical Sciences, Vol. 12, No. 1 (2014) 149–173.
[6] T. C. Lin and B. Eisenberg, Multiple solutions of steady-state Poisson-Nernst-Planck equations with steric effects, Nonlinearity 28 (2015) 2053–2080.
[7] T.L. Horng, T.C. Lin, C. Liu and B. Eisenberg, PNP equations with Steric Effects: a Model of Ion Flow through Channels, The Journal of Physical Chemistry B, 2012, 116 (37), p. 11422-11441.
[8] Tzyy-Leng Horng , Robert S. Eisenberg, Chun Liu, Francisco Bezanilla, Continuum gating current models computed with consistent interactions, 2018, preprint.
當期焦點